techrest.blogg.se - Liner subspace definition

We know from calculus that the sum of continuous functions is continuous.

We know from calculus that 0 ∈ C( R) ⊂ R R.

Let C( R) be the subset consisting of continuous functions. (The equation in example I was z = 0, and the equation in example II was x = y.)Īgain take the field to be R, but now let the vector space V be the set R R of all functions from R to R. In general, any subset of the real coordinate space R n that is defined by a system of homogeneous linear equations will yield a subspace. Then c p = ( cp 1, cp 2) since p 1 = p 2, then cp 1 = cp 2, so c p is an element of W.

Let p = ( p 1, p 2) be an element of W, that is, a point in the plane such that p 1 = p 2, and let c be a scalar in R.

Then p + q = ( p 1+ q 1, p 2+ q 2) since p 1 = p 2 and q 1 = q 2, then p 1 + q 1 = p 2 + q 2, so p + q is an element of W.

Let p = ( p 1, p 2) and q = ( q 1, q 2) be elements of W, that is, points in the plane such that p 1 = p 2 and q 1 = q 2.Take W to be the set of points ( x, y) of R 2 such that x = y.

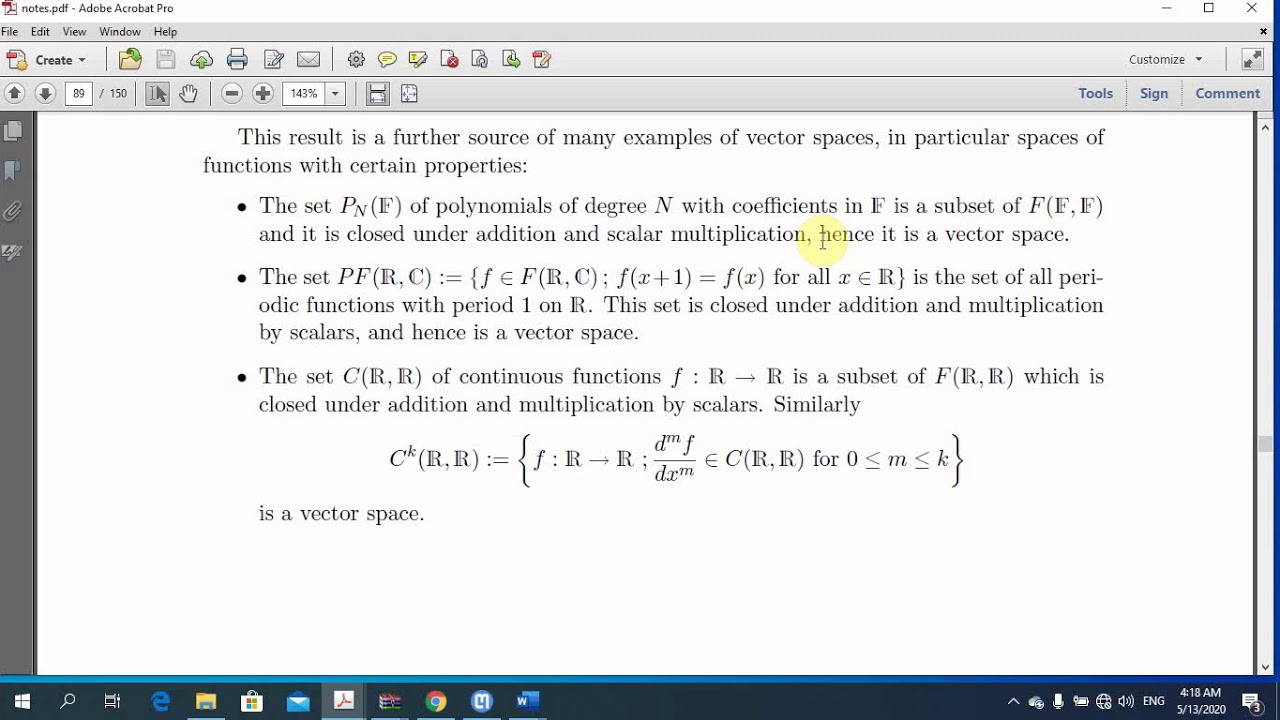
Let the field be R again, but now let the vector space V be the Cartesian plane R 2. Given u in W and a scalar c in R, if u = ( u 1, u 2, 0) again, then c u = ( cu 1, cu 2, c0) = ( cu 1, cu 2,0).Given u and v in W, then they can be expressed as u = ( u 1, u 2, 0) and v = ( v 1, v 2, 0).In the vector space V = R 3 (the real coordinate space over the field R of real numbers), take W to be the set of all vectors in V whose last component is 0. These are called the trivial subspaces of the vector space. Īs a corollary, all vector spaces are equipped with at least two (possibly different) linear subspaces: the zero vector space consisting of the zero vector alone and the entire vector space itself. Equivalently, a nonempty subset W is a subspace of V if, whenever w 1, w 2 are elements of W and α, β are elements of K, it follows that αw 1 + βw 2 is in W. If V is a vector space over a field K and if W is a subset of V, then W is a linear subspace of V if under the operations of V, W is a vector space over K. A linear subspace is usually simply called a subspace when the context serves to distinguish it from other types of subspaces. In mathematics, and more specifically in linear algebra, a linear subspace or vector subspace is a vector space that is a subset of some larger vector space. a 5 × 5 square) is pictured four times for a better visualization The origin (0, 0), marked with green circles, belongs to any of six 1-subspaces, while each of 24 remaining points belongs to exactly one a property which holds for 1-subspaces over any field and in all dimensions. One-dimensional subspaces in the two-dimensional vector space over the finite field F 5.